The List Trifecta, part 2
Sorted data structures to meet your needsIntroduction
In the previous article I introduced the A-List, an "all-purpose" list, which is a cross between a conventional List<T> and an in-memory B+ tree. It also has some interesting features like combining or splitting two large lists in O(log N) time, freezing, fast cloning, and observability.
In this article I'll talk about the sorted "B" data structures based on the A-List concept: The BList<T>, the BDictionary<K,V> and the BMultiMap<K,V>. Here's a class diagram--similar to the diagram in the last article, but with different derived classes:
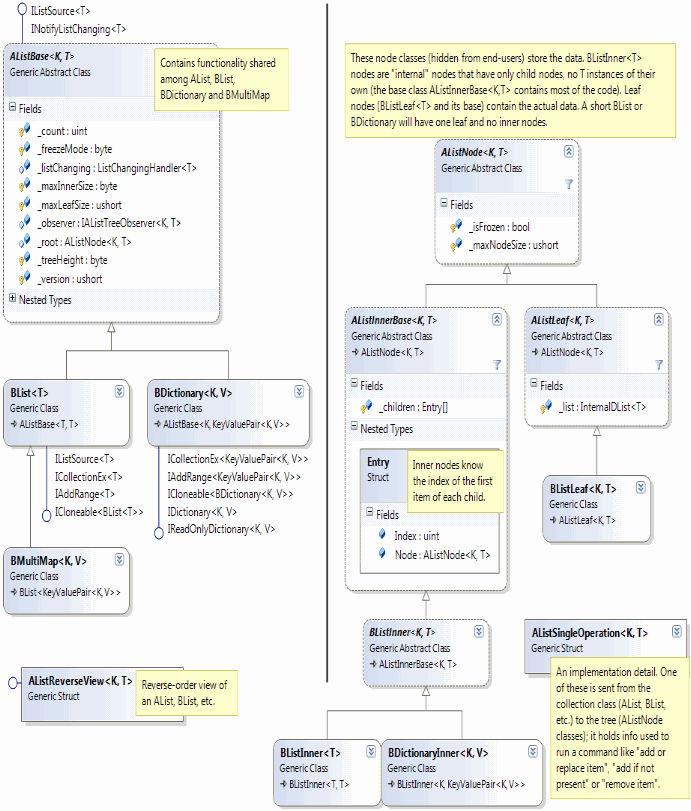
As I said in the first article, data structures in the A-List family (which includes BDictionary, BList and BMultiMap) are tree data structures similar to B+ tree, with one unusual feature: they are indexable; you can write alist[index] (to see how this works, it may help to look at the diagrams in the previous article.)
Growing up as a young software developer, I used a lot of indexed lists and growable arrays all over the place, and occasionally they got very slow when you inserted lots of elements in the middle, or at the beginning, of a long list. In comp-sci speak, building a list of elements, when inserting at random locations, takes O(n2) time, which means it's really damn slow for large n! A-List data structures don't have that problem; they are never slow. They do have higher constant overhead than List<T>, but they don't slow down very much as the list gets bigger.
The basic indexing functionality and management of the tree structure is implemented in the base classes AListBase<T>, AListNode<K,T>, AListInnerBase<K,T> and AListLeaf<K,T>. The new derived classes on the diagram (the ones that start with "B") provide and enforce a constraint that the data must be sorted.
BDictionary: B is for Better
The .NET framework has a class called SortedList<TKey,TValue>. You should never, ever use that class to build a sorted list! Unless, that is, the data was already sorted to start with, in which case you still don't need SortedList.
The problem with SortedList is, of course, performance. It takes O(n2) time to build a SortedList from n key-value pairs in random order. Instead, you should use SortedDictionary<TKey,TValue> or BDictionary<K,V>, depending on whether you need BDictionary's numerous features or not.
BDictionary<K,V> is very much like SortedList, just much faster, and with a heck of a lot more features. Like SortedList, BDictionary is a dictionary of items kept in sorted order, and it allows access to items by index. It is efficient for all operations: Add, Remove, IndexOf, ContainsKey, FindLowerBound, FindUpperBound, and the indexer all run in O(log N) time. You can specify a key-comparison delegate when you construct it, so the type K does not have to be directly sortable and you don't have to sort in the "natural order" for K.
It also supports the following operations that SortedList does not:
FindLowerBound(k): Finds the lowest index of an item whose key that is equal to or greater thank. It behaves like the standard C++ function lower_bound.FindUpperBound(k): Finds the index of the first item in the list that is greater thank(this tends to be less useful thanFindLowerBound.)AddRange(list),RemoveRange(list),RemoveRange(start, count)this[key, defaultValue]: finds the value associated with a key. If that key is not found, returnsdefaultValue.Clone(): creates a copy in O(1) time (this technique is explained in the part 1)CopySection,RemoveSection: duplicates or removes any portion of the list in O(log N) time.AddIfNotPresent(k, v): Adds the specified pair only if the key is not already present in the dictionary.ReplaceIfPresent(k, v): Replaces the value associated with k, if it already exists in the dictionary.SetAndGetOldValue(k, ref v): Gets the old value associated withk, if there is one, then setsthis[k] = v.
And, like all classes derived from AListBase, BDictionary (and BList and BMultiMap) supports RemoveAll(lambda), fast Clone(), Freeze(), Slice(), ReverseView and the ListChanging event.
Spot the design flaw?
BDictionary<K,V> will give you a small problem if K just happens to be int, because there is a this[K] indexer and also a this[int] indexer. So if you call dict[4], does that get the fifth element (of type KeyValuePair<K,V>), or the V value associated with the key 4? Well, the two indexers exist in different classes: this[K] is in the derived class, and this[int] is in the base class. So dict[4] will get the V value associated with the key 4, and you can get the fifth element with an upcast: ((AListBase<int,KeyValuePair<int,V>>) dict)[4]. Okay, it's a bit clunky, but it works.
BList and BDictionary: I lied. B is for B+ tree.
BList<T> is simply a sorted list (like all other A-List classes, it is structured as a B+ tree). Unlike SortedList<TKey,TValue> and BDictionary, it is just a list, not a dictionary. BList permits duplicate items, so it is not a "set" class. It allows you to specify a comparison delegate when you construct it, so the type T does not have to be directly sortable and you don't have to sort in the "natural order" for T.
BList has all the same features of BDictionary, just without that pesky distinction between "keys" and "values". There's not much else to say about BList, so let's move on...
BMultiMap<K,V>, derived from BList<KeyValuePair<K,V>>, is a special kind of dictionary that permits duplicate keys (as well as duplicate values). Or, viewed from a different perspective, it allows multiple values to be associated with a single key. It is comparable to the C++ std::multimap class, although it does some things more easily (for instance you can avoid duplicate key-value pairs using AddIfUnique().)
To use BMultiMap<K, V>, both K and V must be comparable (unlike BDictionary which only needs the key type K to be comparable). This requirement is needed for some methods, such as AddIfUnique and Remove(KeyValuePair<K,V>) (inherited from BList), to work correctly. If you want to use a V that is not actually comparable, you could use a comparison function that pretends all Vs are equal (by always returning 0); just be aware that any methods that try to distinguish Vs from each other will behave as if they are all equal! You could also sort based on GetHashCode(), just be very, very careful to handle the possibility that two unrelated objects have the same hashcode (IndexOfExact() sometimes help deal with this case).
BMultiMap provides the illusion that it is a dictionary of sorted collections. The indexer this[K] returns a BMultiMap<K,V>.Values structure, which implements ICollection<V> and provides access to all the values associated with a particular key. To add a new key-value pair, you can either call Add(K, V) on the multimap itself, or this[K].Add(V). Similarly you can remove all the values for a key using either RemoveAll(k) or this[K].Clear().
In reality, BMultiMap is not really a dictionary of collections, it is just a single sorted list. The list is sorted first by key, and then by value, so all the values associated with a particular key k are adjacent to each other in the list. The Values structure calls FindLowerBound and FindUpperBound to figure out where this "sub-list" begins and ends inside the list as a whole.
Please note that the collection returned by this[K] is not indexable; you can't write this[key][0], for example, although you can of course use this[K].First(), relying on the LINQ extension method First(), and you can use a foreach loop to iterate over the values for a particular key. The Values collection doesn't have an indexer because it would be either incorrect or inefficient. Incorrect, because if it cached the location of the first item to improve performance, this location would change whenever items were added or removed in a different part of the map. On the other hand, if Values does not cache the location of the first item (and it doesn't), a loop like this could be very slow:
var values = multimap[key];
for (int i = 0; i < values.Count; i++) {
DoSomethingWith(values[i]);
}
First of all, measuring the Count requires the multimap to be searched twice: once to find the lower bound (the location where the Values start for the specified key) and once more for the upper bound (where the Values for this key end). And then, because these indexes are not cached, values[i] would have to find the lower bound again, then looking up item at offset i from the lower bound, and finally check to make sure that the key of this item is the same (if not, it would have to throw IndexOutOfRangeException). Since all this work would slow down your code, no indexer is provided. Use a foreach loop instead; the lower bound will be computed only once, before the first iteration of the loop, and the upper bound is not computed (instead, the Values enumerator keeps scanning forward in the B+ tree until the key of the current KeyValuePair changes).
When calling the indexer this[K], the specified key does not have to exist in the collection. If it doesn't exist, the indexer returns an empty collection (by the way, do not call this[k].Count unnecessarily; remember, two searches are required to measure the collection's length.)
BMultiMap has several methods that you might find useful:
FindLowerBound(k): just likeBDictionary's method by the same name, it finds the first element equal or greater thank. Likewise,FindUpperBoundfinds the first element greater thank.FirstIndexOf(k): likeFindLowerBound(k)except that it returns-1ifkis not found.AddIfUnique(k, v): adds a key-value pair if there is not already a pair that compares equal to the new one.Remove(k, max): removes the firstmaxvalues associated with the specified keyRemoveAny(k): removes any one pair that has the specified key (it's similar toRemove(k, 1)but runs slightly faster and you can't predict which one it will remove)RemoveAll(k): removes all key-value pairs with the specified key.IndexOfExact(k),FindLowerBoundExact(k): finds the index of a valuekthat not only compares equal using the comparison function, but also compares equal according toobject.Equals. This can be useful if the comparison function only sorts based on part of the object, but you'd also like to match the rest of the object that the comparison function ignores.
In Conclusion
So there you have it, a bunch of sorted data structures.
In terms of performance, I haven't benchmarked any of these data structures, but I can predict with confidence that:
- The
AList<T>family of data structures is generally slower thanList<T>for indexing, enumerating (foreach), adding items at the end, removing items from the end, and any operation involving a short list (less than about 100 items). - The
AList<T>family of data structures is generally faster thanList<T>for inserting and removing at random locations, merging lists, splitting lists, cloning, etc., in lists that are very long. - The
AList<T>family of data structures will generally use slightly more memory thanList<T>(but significantly less memory thanHashSet<T>). BDictionary<K,V>is generally much faster thanSortedList<K,V>for lists of significant size (above 50 items).BList<T>andBMultiMap<K,V>have similar performance asBDictionary<K,V>.BDictionary<K,V>will be slower thanDictionary<K,V>but it will generally use less memory.- I don't know whether
BDictionary<K,V>is faster or slower thanSortedDictionary<K,V>but it will definitely use less memory. BMultiMap<K,V>has the same memory requirements asBDictionary<K,V>, and it will use much less memory thanDictionary<K,List<V>>.
In part 3, I'll talk about the much simpler the new DList<T> and DListInternal<T>SparseAList<T> data structure, and show you some benchmark results.
Update: Part 3 is ready.
Where to get it: ALists are part of Loyc.Collections.dll which you can get in the NuGet package "LoycCore". The libraries are compiled for .NET 3.5, .NET 4 and .NET 4.5. In the source code on GitHub, the solution file should open in VS 2010, VS 2012 and VS 2013.